Introduction #
Hash tables are the diva of data structures. No other data structure offers the same opportunity for bugs to be introduced during optimization. In this blog post, we explore how hash tables are used in ClickHouse. We'll show how zero-cost abstractions work in modern C++ and how to get a variety of data structures from a common codebase with a few little tricks. Based on common building blocks, we can build a fast-cleaning hash table, several types of LRU caches, lookup tables without hashes, and hash tables for strings. We also show how to ensure the best performance in specific scenarios and how to avoid making mistakes when testing performance. These are the low-level optimizations we love at ClickHouse!
First, let's discuss why hash tables are needed, where they can be used in a database, and how to make them optimal. Then we will look at the benchmarks of various hash tables on the internet and explain how to implement them correctly. Finally, we will talk about our zero-cost C++ framework which produces ideal hash tables for specific use cases.
Applications in ClickHouse #
ClickHouse is known for its ability to aggregate huge amounts of data at lightning speed. Aggregation in SQL is expressed by the GROUP BY clause. Most databases, including ClickHouse, implement GROUP BY using some variant of the hash aggregation algorithm in which the input rows are stored in a hash table with the grouping columns as key. Choosing the right kind of hash table is critical for performance. It depends on the data type of the grouping columns (e.g. fixed-width integers, variable-width strings, ...), the number of unique keys, their total number, and other factors. ClickHouse has over 40 different optimizations for the GROUP BY clause, with each of them using a highly optimized hash table in a different way and exploiting a powerful framework which generates the best hash table for the job!
If we will say that we have only 1 hash table, that would be incorrect. We have a lot of hash tables, that are build around flexible powerful framework. These variants are primarily used in the execution of GROUP BY and JOIN operations.
A hash table is a data structure that provides constant average performance for insert, lookup and delete operations. Deletion is not important to us for the GROUP BY aggregation scenario.
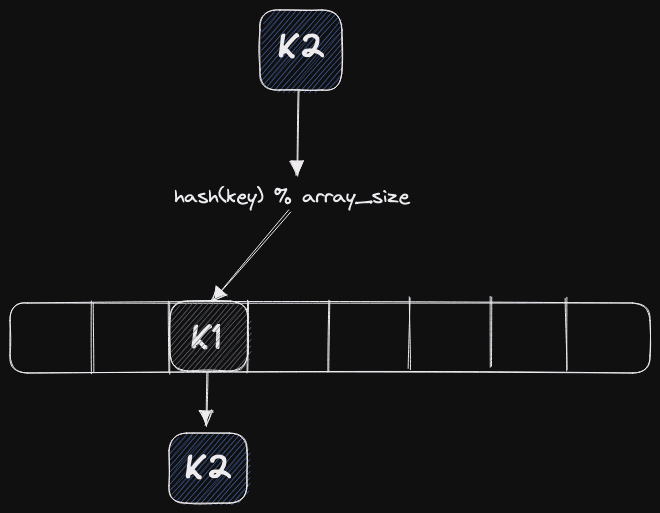
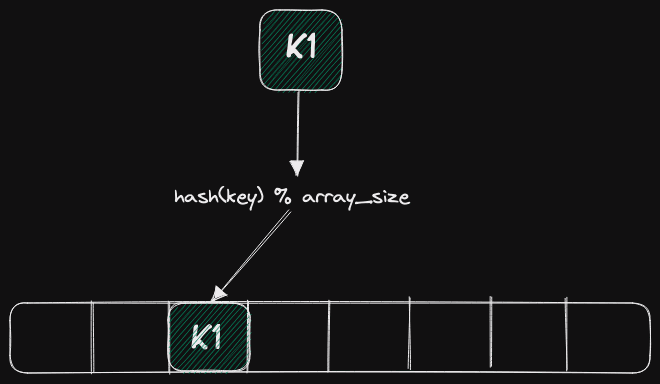 Let's look at the above diagram. Most developers will learn how a hash table is structured from early computer science courses. We take a certain key that we want to insert, hash this using a hash function, and compute a position for insertion into an array using the remainder from the division of the array's length.
Let's look at the above diagram. Most developers will learn how a hash table is structured from early computer science courses. We take a certain key that we want to insert, hash this using a hash function, and compute a position for insertion into an array using the remainder from the division of the array's length.
Hash table design #
Hash tables require many design decisions at different levels and are subtly very complex data structures. Each of these design decisions has important implications for the hash table on its own but there are also ramifications from the way multiple design decisions play together. Mistakes during the design phase can make your implementation inefficient and appreciably slow down performance. A hash table consists of a hash function, a collision resolution method, a resizing policy, and various possibilities for arranging its cells in memory.
Choosing a Hash Function #
Let's start by choosing a hash function. This is a very important design decision where many people often make a mistake due to the number of potential choices, all of which appear to produce equally good random values. We'll outline the main problems with this decision-making process.
First of all, for integer types, it is quite common for many people to use the identity hash function. This is wrong as the distribution of real data is not the same, and you will have a high number of collisions. Furthermore, some hash functions are optimized for integers, use them instead of general-purpose hash functions if your data allows it. Also, do not use various cryptographic hash functions unless you expect to be attacked since these are more computationally expensive. For example, suppose you use the cryptographic Sip Hash function with a throughput of around 1 GB/s vs. the City Hash function at about 10 GB/s. This means that the throughput of your table will be limited to 1 GB/s.
Also, don't use legacy hash functions like FNV1a because they are slow and provide poor distribution relative to competitors. This specific hash function is used in the GCC standard library and is deprecated. The SMHasher repository on GitHub contains tests of various hash functions and shows that FNV1a fails to pass any serious testing.
In ClickHouse, by default, we utilize hash functions that, despite having a relatively bad distribution, are good for hash tables. For example, for integer types, we use CRC-32C. This hash function takes very little CPU time and is very fast as it is implementable with dedicated instructions which use only two to three cycles. For strings, we use our custom hash function built on CRC-32C. If you do not use it, you can use something standard such as Farm Hash.
Collision Resolution #
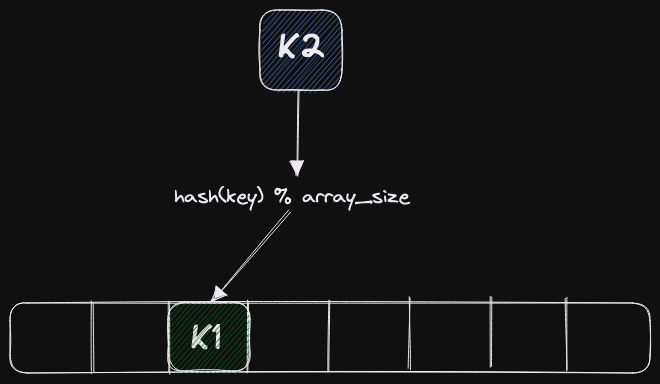
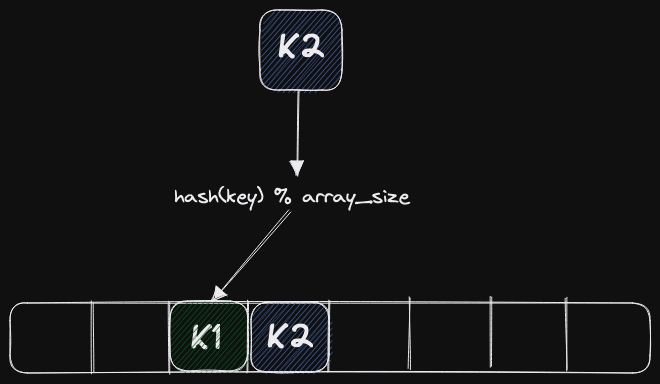
Let's talk about collision resolution. In any hash table, by the birthday paradox, the situation will arise that the same key falls into the same slot. Suppose we inserted the key K1, and it got into the third slot of the table. Now we are trying to insert the K2 key, and according to the remainder of the division, it falls into the same slot as shown above. We need to figure out what to do with it next. There are several ways to resolve this situation.
The first way is to use chaining, where the table cell will use a list or an array, and we will put the next key in the same cell using the underlying data structure.
Alternatively, we can use the method of open addressing. In this case, we put the key in one of the following table slots.
There are more complex ways, such as Cuckoo hashing or two-way hashing. However, these have a problem: they are usually difficult to implement, require additional fetches from memory, and usually slow down at scale. For example, even a lot of code on the hot path significantly slows down lookups in the hash table.
 Let's start with the simplest method - the chain method. This utilizes a list for keys which hash to the same cell. Assuming the first key has been inserted, the second key is appended to a list beneath this first key. Later during lookup both the main cell and its child list are checked for the presence of a key.
Let's start with the simplest method - the chain method. This utilizes a list for keys which hash to the same cell. Assuming the first key has been inserted, the second key is appended to a list beneath this first key. Later during lookup both the main cell and its child list are checked for the presence of a key.
This is how the std::unordered_map is used. Why is this method not effective? It is not cache-local, which will cause poor performance. Its effectiveness is that it will work in all cases and not be very picky about the hash function being used. It will also work even with a high load factor. But, unfortunately, it will load the allocator very heavily since even calling any function on hot path lookup in the hash table will be very expensive. As a result, all modern hash tables use the open address method.
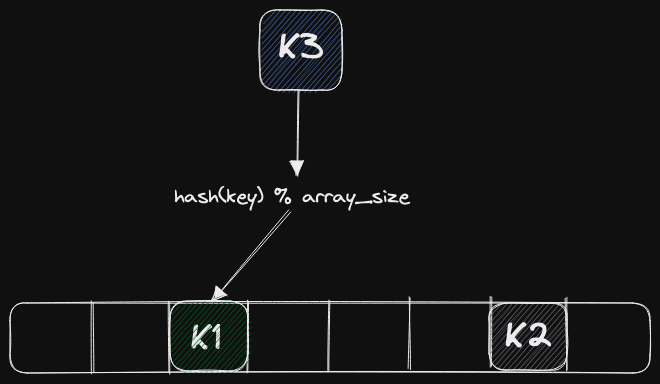
 In this blog, I will talk about three hash tables worth paying attention to. Two of them are Google Flat Hash Map and Google Abseil Hash Map. Abseil is one of Google's newer frameworks, taking a slightly different approach to hash tables. We will also talk about the hash table in ClickHouse. And all these hash tables use the open addressing method. For this method, when the second key is hashed and allocated to the same slot as the first one, we put it in one of the next slots in the array - as shown above.
In this blog, I will talk about three hash tables worth paying attention to. Two of them are Google Flat Hash Map and Google Abseil Hash Map. Abseil is one of Google's newer frameworks, taking a slightly different approach to hash tables. We will also talk about the hash table in ClickHouse. And all these hash tables use the open addressing method. For this method, when the second key is hashed and allocated to the same slot as the first one, we put it in one of the next slots in the array - as shown above.
The choice of the next slot depends on many factors. We could use linear probing; that is, we simply choose the next slot. There may be quadratic probing where we select the next slot with a multiplier of 2, i.e., one, two, four, eight, and so on. This gives an ideal cache locality since data is fetched by cache lines in the processor. This means that one hash key lookup translates to only one fetch from memory. The main issue with this method is it needs a good hash function that fits your data.
Let's imagine that we have chosen a bad hash function. It is easy to assume that there will be moments when clusters form in our array that "stick" together. When this situation arises, we will start checking keys unrelated to the value we are looking for. This method is also poorly suited for large objects as they will kill all cache locality, making its primary advantage redundant. How do we address this issue? We serialize large objects somewhere and store pointers to them in a hash table.
Another very important concept is resizing. First, you need to decide how many times to resize. There are two ways. The first is to resize by powers of two. This method is good in that the minimum time should be spent on division during table lookup, with it executing in nanoseconds if the table is present in the cache. If you don't use a power of two, division will occur, which is very expensive. However, if the table size is always a power of two the expensive division operation (%), which is needed to determine the position of the hash value in the hash map, can be replaced by a cheap bit shift operation (<<). There is also a more theoretical justification for using a power that is close to a power of two but also a prime number. The downside is that you need to figure out how to avoid division. For this, we can use some kind of constant switch or a library like libdivide.
Concerning the load factor, ClickHouse and all Google hash tables, except for the Abseil Hash Map, use a load factor of 0.5. This is a good load factor that you can use in your hash tables. The Abseil Hash Map uses a load factor of around 0.9.
 The most interesting thing is the way cells are arranged in memory, with decisions important to keep the hash table functional.
Why do we need a special away to place cells in memory? As soon as someone first starts trying to write their open addressing hash table, they are faced with such a situation. Imagine: you are writing code and trying to insert and handle a situation where your second key falls into the first slot, but a collision occurs. We need to figure out what to do next.
The most interesting thing is the way cells are arranged in memory, with decisions important to keep the hash table functional.
Why do we need a special away to place cells in memory? As soon as someone first starts trying to write their open addressing hash table, they are faced with such a situation. Imagine: you are writing code and trying to insert and handle a situation where your second key falls into the first slot, but a collision occurs. We need to figure out what to do next.
First of all, we will have to loop through the cells, deciding if each cell is empty, whether we can write to it or if its been deleted. Assuming the memory is initialized, we need to be able to distiguish between the cell being empty (i.e. not assigned a value or empty as the result of a delete) or simply containing a Null value e.g. in ClickHouse we support nullable types.
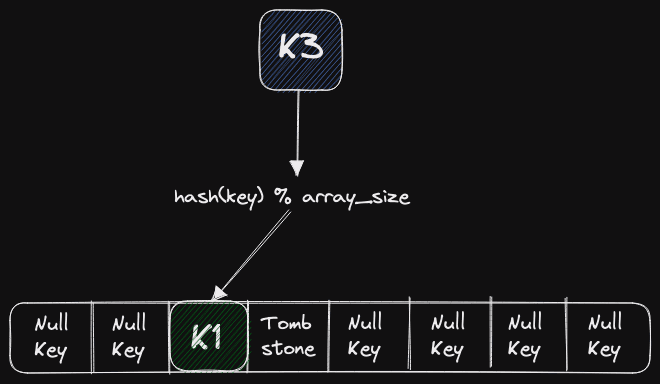 There are several options in this situation. The first option is to ask the user of the hash map to provide some key value to indicate an empty cell, as well as a tombstone key for deleted cells. These values can never be inserted into the hash table by the user, i.e., it is not in the real data, and hence we can use it to identify that a cell is empty or deleted.
This method is used in Google Flat Hash Map. The main disadvantage of this method is that we have to make the client choose some key that will not be presented in their data. Sometimes it's easy to find the key, and sometimes hard, but in general, it complicates the API. This is roughly visible in the picture: there are slots in the hash table, and some of them are null keys, and some are tombstones. This way, we can safely check that this slot is empty.
There are several options in this situation. The first option is to ask the user of the hash map to provide some key value to indicate an empty cell, as well as a tombstone key for deleted cells. These values can never be inserted into the hash table by the user, i.e., it is not in the real data, and hence we can use it to identify that a cell is empty or deleted.
This method is used in Google Flat Hash Map. The main disadvantage of this method is that we have to make the client choose some key that will not be presented in their data. Sometimes it's easy to find the key, and sometimes hard, but in general, it complicates the API. This is roughly visible in the picture: there are slots in the hash table, and some of them are null keys, and some are tombstones. This way, we can safely check that this slot is empty.
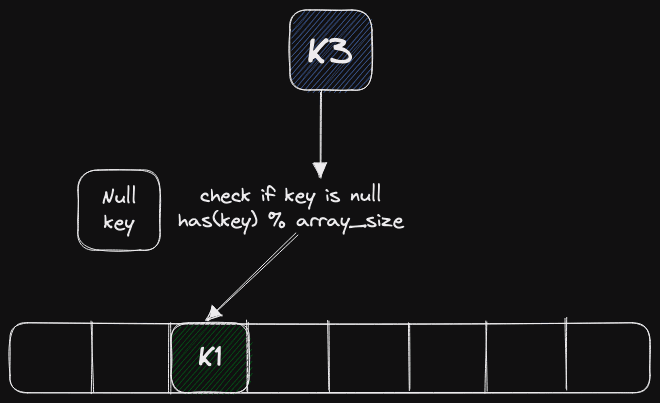 A more advanced method is used by us at ClickHouse and is shown above. We do not keep Null cells in the hash table. We have some special cell for the Null element, and we keep it separate. Before inserting or looking up the hash table, we first check if the value is Null or not and process it separately. The downside is that an additional branch appears, but in practice the branch predictor in the CPU is very effective at hiding the extra costs such that our performance is not affected.
A more advanced method is used by us at ClickHouse and is shown above. We do not keep Null cells in the hash table. We have some special cell for the Null element, and we keep it separate. Before inserting or looking up the hash table, we first check if the value is Null or not and process it separately. The downside is that an additional branch appears, but in practice the branch predictor in the CPU is very effective at hiding the extra costs such that our performance is not affected.
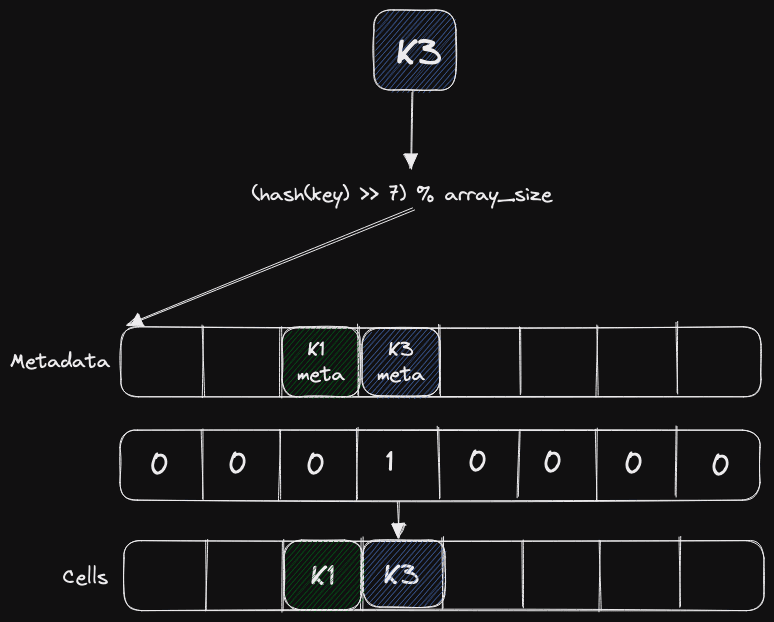 There is also a rather complicated way, which is used in the newest hash table from Google. To arrive at this method, you need to start with simpler cases. For example, we want somewhere to keep information about whether a cell is deleted or empty. We will waste additional memory if we try to write this into a hash table. So, we will keep it somewhere else, for example, in some metadata.
There is also a rather complicated way, which is used in the newest hash table from Google. To arrive at this method, you need to start with simpler cases. For example, we want somewhere to keep information about whether a cell is deleted or empty. We will waste additional memory if we try to write this into a hash table. So, we will keep it somewhere else, for example, in some metadata.
But since it turns out that we need only two bits, it is expensive to spend them on this information. We can try a whole byte, but what about the rest of the bits? In the Google implementation, the top 53 bits of the hash function are used to search for cells with metadata, and the bottom bits of the hash functions are in the metadata.
Why might this be useful? We can put this data in registers and quickly check to see if we should look at the associated cells - for example, using SSE instructions.
Benchmarks #
If you decide to see which hash table is the best, then every second person on the Internet has written their fastest hash table. If you start to dig deeper, you will see that this is not true. Many benchmarks don't cover important things and don't use any specific scenarios. It is thus not clear if the hash table is fast or not.
What are the main problems with benchmarks? They are often made not on real data but on random numbers. The distribution of random numbers does not correspond to real data. Also, quite often, no specific scenario is considered. Just as often, they don't show the benchmark code, only displaying various kinds of graphs and making it impossible to repeat the benchmark.
How should benchmarks be done? They need to be done on real data and on real scenarios. In ClickHouse, the real scenario is data aggregation, and we take the data itself from a web analytics dataset you can download it from our website.
Now let's take a look at the benchmarks and try to analyze how different design decisions affect hash table performance.
The following results are based on a WatchId column containing around 2,071,4865 unique values. These do not fit in CPU caches and take up about 600 MB, forcing access to main memory. Timings here represent the total run time to aggregate all values.
| Hashtable | Time (seconds) |
|---|---|
| ClickHouse HashMap | 7,366 secs |
| Google DenseMap | 10,089 secs |
| Abseil HashMap | 9,011 secs |
| std::unordered_map | 44,758 secs |
If we look at this benchmark, we will see that ClickHouse and hash tables are way ahead of std::unordered_map. Why? Because, as I said, std::unordered_map is not cache-local; specifically this data is not placed in the Lx caches. We can look at this with perf stat to confirm our assumption that std::unordered_map has more cache misses, which slows it down.
| Hashtable | Cache misses |
|---|---|
| ClickHouse HashMap | 329,644,616 |
| Google DenseMap | 383,350,820 |
| Abseil HashMap | 415,869,669 |
| std::unordered_map | 1,939,811,017 |

We can also look at numbers that confirm the higher cost of accessing main memory vs. L1 or L2 caches. We can assume that in order for a hash table to work at maximum speed, it must optimize for cache locality.
Let's take a slightly different benchmark, in which all data goes into caches. In this case, we see that std::unordered_map doesn't slow down as much anymore. In thise case, we use a RegionID column which has repeating values from a set of 9040 unique values which fit into Lx caches.
| Hashtable | Time (secs) |
|---|---|
| ClickHouse HashMap | 0.201s |
| Google DenseMap | 0.261s |
| Abseil HashMap | 0.307s |
| std::unordered_map | 0.466s |
C++ hash table design #
So far, we have focused on the algorithmic design of the solution. But for all this to work well, we need to develop a flexible and powerful C ++ wrapper.
Our hash table wrapper utilizes a policy-based design, i.e. each design choice becomes a separate part of the hash table's interface. The main interfaces are the hash function, the allocator, the cell (which is an important element in our table), the grower (the interface for the resize policy), and the hash table itself, which combines all these components together.
Let's start with the hash function. This is the same interface as std::hash introduced in C++11, nothing new.
template <typename T>
struct Hash {
size_t operator () (T key) const
{
return DefaultHash<T>(key);
}
};
The allocator is a slightly modified interface of the standard library allocator since our version supports realloc. Why do we need realloc? On Linux, we use mmap and mremap for large hash tables. To support this, we need to provide a realloc method in our interface.
The folowing allocator uses mmap and mremap for large memory blocks.
class Allocator
{
void * alloc(size_t size, size_t alignment);
void free(void * buf, size_t size);
void * realloc(void * buf, size t old size, size_t new size);
};
There is also an allocator that allocates memory on the stack from the beginning when we use a custom policy for it.
AllocatorWithStackMemory<HashTableAllocator, initialbytes>
The hash table cell is a full-fledged element of our hash table; you can write a hash into it, get a hash from it, and check if it is empty. Also, the cell itself can provide information for the hash table i.e. it understands what is inside the hash table since it is parameterized by its state.
template <typename Key, typename Mapped, typename HashTableState>
struct HashTableCell {
...
void setHash(size_t hash_value);
size_t getHash(const Hash & hash) const;
bool isZero(const State & state);
void setZero();
...
};
The following are the interfaces for our resizing policy, with methods for getting a place in the hash table, moving to the next element, checking whether inserting the next element will lead to table overflow, and resizing itself. Let's define them in the code.
struct HashTableGrower
size_t place(size_t x) const;
size_t next(size_t pos) const;
bool willNextElementOverflow() const;
void increaseSize();
};
The hash table is generated from a C++ template which combines all of these interfaces by inheriting from them. Unlike composition at runtime using virtual methods, this approach ensures optimal performance as the compiler is able to optimize each of the generated hash tables individually.
template
<
typename Key,
typename Cell,
typename Hash,
typename Grower,
typename Allocator
>
class HashTable :
protected Hash,
protected Allocator,
protected Cell::State;
protected ZeroValueStorage<Cell::need_zero_value_storage, Cell>
For example, how do we use zero-value storage? If one of the base classes contains no data, we don't waste extra memory storing it. For example, we mentioned above that ClickHouse generates the zero value cell separately and places it in a special zero-value storage. But this is only necessary in some cases. Suppose we don’t need it, in which case zero value storage is a specialization that does nothing, the compiler removes unnecessary code, and nothing slows down.
template ‹bool need_zero_value_storage, typename Cell>
struct ZeroValueStorage;
template <typename Cell>
struct ZeroValueStorage<true, Cell>
{
...
};
template <typename Cell>
struct ZeroValueStorage<false, Cell>
{
...
};
What does a custom resizing policy gives us? A custom resizing policy with a fixed size, and without resolving hash collisions, produces hash tables that are perfectly suitable for caching recent elements. Using a resizing policy with a step not equal to one, we can get, for example, quadratic probing, which can be convenient for checking various benchmarks.
The ability to store state in a cell helps us store useful information in a cell, such as a hash value. What can it be useful for? For the case where we don't want to recalculate the hash function in case of string hash tables.
struct HashMapCellWithSavedHash : public HashMapCell
{
size_t saved_hash;
void setHash(size_t hash_value) { saved_hash = hash_value; }
size_t getHash(const Hash &) const { return saved_hash; }
};
We can also make a hash table that can be quickly cleared. It is useful when we have a huge hash table, we have already filled it with data, and now we want to reuse it. To delete all elements in the hash table we use the version of the table as the state - we store the version both in the cell and in the table itself. When checking if the cell is empty, we just compare the version of the cell and the hash table. If we need to do a quick delete, we increment the hash table version by one. This is more performant than trying to delete all the cells in the hash table, which would require us to run through it and incur significant cache misses - causing poor performance.
strut FixedClearableHashMapCell
{
strut ClearableHashSetState
{
UInt32 version = 1;
};
using State = ClearableHashSetState;
UInt32 version = 1;
bool isZero(const State & st) const { return version ! = st.version; }
void setZero() { version = 0; }
}
Another interesting trick is LRU Cache. This is an implementation of the LRU exclusion policy. Usually, this is implemented as a doubly-linked LRU list and a hash table which provides fast mapping from key to the position in the list. Every time we refer to a specific key, we need to move the value to the "most recent" end of the list and update the value's mapping in the hash map. If an element is not stored in the LRU cache yet, we evict the element at the "least recent" end of the list and insert the new one instead. When the list becomes full, we remove the element from the beginning of the list. This way the list will always contain the most recent elements.
An implementation of the LRU cache using a separate list and a hash table are not optimal because it uses two containers. In the case of ClickHouse, we figured out how to do this in a single container. In a hash table cell, we store a pointer to the next and previous element resulting in a doubly linked list right inside the hash table.
struct LRUHashMapCell
{
static bool constexpr need_to_notify_cell_during_move = true;
static void move(LRUHashMapCell * old_loc, LRUHashMapCell * new_loc);
LRUHashMapCell * next = nullptr;
LRUHashMapCell * prev = nullptr;
};
To implement this, we store two pointers and use the Boost Instrusive library. Below we show the most important parts of this. We make an intrusive list and use it as a list. The fact that we declared pointers to the next and previous element in the cell is enough for us to create an intrusive list on the top of the cells.
using LRUList = boost:: intrusive:: list
<
Cell,
boost::intrusive::value_traits<LRUHashMapCellIntrusiveValueTraits>,
boost::intrusive::constant_time_size<false>
>;
LRUList ru_list ;
We have several specialized hash tables for various scenarios. For example, small table is a hash table, which is an array. How can it be useful? It is placed in the L1 cache and it implements the hash table interface. This is useful if we need to implement a simple algorithm.
template <typename Key, typename Cell, size_t capacity>
class SmallTable : protected Cell:: State
{
size_t m_size = 0;
Cell buf[capacity];
...
}
We also have a more interesting hash table - the string hash table. It was contributed to us by a graduate student from China. These are four hash tables for strings of different lengths, for which we use different hash functions. More specifically, this hash table consists of 4 hash-tables:
- for strings 0-8 bytes in size
- for strings 9-16 bytes in size
- for strings 17-24 bytes in size
- for strings bigger than 24 bytes
Another very interesting hash table is a two-level hash table. It consists of 256 hash tables. Why might this be necessary if you are not a fan of hash tables? When we, for example, do a GROUP BY operation, we want to do it in multiple threads. Therefore, we need to populate the tables and then merge them. We could use lock-free hash tables, but no one on our team likes lock-free, so we use two level hash tables.
This works by creating two level hash tables in each thread. For example, we get a matrix of 256 columns (tables) and four rows (streams) if we have four streams. We are inserting data into one of these tables. For example, we make the distribution according to such a formula, as shown below. Then, when we need to join tables, we use minimal synchronization and join them by columns. In the end, nothing slows down here.
size_t getBucketFromHash(size_t hash_value) {
return (hash_value >> (32 - BITS_FOR_BUCKET)) & MAX_BUCKET;
}
So, we have written our own rather flexible and powerful framework for implementing hash tables. From it, you can get hash tables for different scenarios.
I want to confess: I really love hash tables. For those who manage to improve our benchmark - for example, make a hash table that is faster than ours we will offer a unique "ClickHouse does not slow down hoodie"!



